↓

[Masters Project] GPU-Optimised Linear Algebra for Small Matrices

··
Sihan Yu
Sihan Yu

Repo (my supervisor’s GitHub): Github – BatchedKernels.jl

My master’s project focuses on accelerating linear algebra operations on large batches of small matrices using GPUs. This implementation outperforms state-of-the-art libraries such as JAX by as much as 30x.

Overview
#

Modern GPU-accelerated libraries are primarily optimised for large matrices, as large matrices typically come with larger workloads, and GPU parallelisation is more necessary.

However, there are use cases where operations on large batches of small matrices are performed, and due to the large batch sizes, the overall workloads may still be significant. When performing operations on small matrices, existing libraries do not fully utilise the hardware’s capabilities, and if the batch size is large enough, existing implementations may be prohibitively slow.

This project investigates, designs, and implements a hardware-aware GPU execution model for large batches of small-matrix operations, optimised for multi-step algorithms, starting from my supervisor’s proof-of-concept. This is made accessible for regular users via automatic GPU kernel generation similar to JAX vmap.

Achieved performance
#

The figure below shows the average per-matrix computation time for different matrix dimensions D, for a dummy algorithm (Kalman filter covariance update was used here), and compares it against other state-of-the-art implementations.

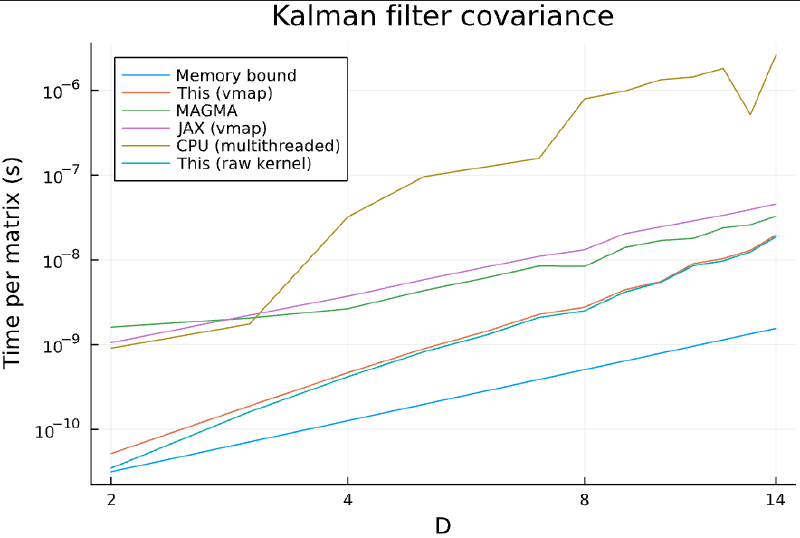
Result

Compared to existing implementations:

  • 2.5x – 30x speedup over JAX vmap
  • 2x – 45x speedup over MAGMA (a C++ library for optimised batched small-matrix operations)
  • 10x – 300x speedup over a 48-core multithreaded CPU-implementation

Technical background
#

The key to achieving such speed is exploiting the fact that very small matrices allow entire matrices to reside in GPU shared memory, across different operations during multi-step algorithms. This allows data reuse and avoids global memory traffic for intermediate results. For sufficiently small matrices, this is actually the dominant cost, especially for multi-step algorithms.

Furthermore, each GPU warp can be assigned exclusive responsibility for a fixed group of matrices, which makes the whole execution completely warp-independent. Shared memory is also separated to regions, each region only accessed by one warp. As a result, warps never need to be synchronised, even across multiple operations. This allows for highly efficient kernel fusion.

To make this as efficient as possible, the shared memory layout is carefully designed to guarantee bank-conflict-free accesses for both row-wise and column-wise matrix operations. This is achieved by having one thread process a full row/column instead of one element. This is made possible by designing the shared memory to store matrices in an interleaved manner (1st element of matrix 1, 1st element of matrix 2, …) instead of each matrix contiguously. Alongside appropriate padding, this also ensures each warp accesses distinct memory banks during a lockstep, allowing maximum shared memory bandwidth, essential to achieving near-optimal performance.

To make this accessible, I implemented a lightweight compiler that automatically generates specialised, fused kernels. Without this, users would have to manually implement any custom algorithm using low-level batched primitives, requiring careful reasoning about warp-level execution and the shared memory layout. This is exposed to users via a familiar JAX vmap-like interface, allowing users to write ordinary functions while benefitting from highly specialised hardware-aware kernels.

This project is implemented in Julia and CUDA.jl.

Ongoing work & roadmap
#

Over the remainder of the academic year, I am continuing to extend this project, primarily focusing on adding support for more linear algebra operations. So far only the operations involved in the Kalman filter have been implemented.